Mathematik
'Vollkommene Zahlen' sind Zahlen, bei denen die Summe der Teiler wieder die Zahl selbst ergibt. Zusätzlich lassen sich diese Zahlen aus einer lückenlosen Reihen-Summe der Zahlen von 1 bis n bilden.
Der Entdecker dieser Eigenschaften soll Pythagoras gewesen sein.Und Euklid (Griechischer Mathematiker um 300 v. Chr.) soll dazu herausgefunden haben, dass vollkommene Zahlen immer wie folgt aufgebaut sind (siehe Spalte Euklid):
| Zahl | Teiler | Reihen-Sa | Euklid | x*(2x-1) | ??? |
| 6 | 1,2,3 | 1+2+3 | |||
| 28 | 1,2,4,7,14 | 1+2..7 | 22*(23-1) | 4*7 | 13+33 |
| 496 | ... | 1+2..+31 | 24*(25-1) | 16*31 | 13+33+53+73 |
| 8128 | ... | 1+2..+127 | 26*(27-1) | 64*127 | 13+33..+153 |
Römische Zahlen
Sehr große röm. Zahlen:Die gebräuchlichste Schreibweise für große röm. Zahlen war und ist wohl die mit Oberstrich für die Multiplikation mit 1000.
Also:
C (mit einem Oberstrich)
= 100 x 1000 = 100.000
M (mit einem Oberstrich)
= 1000 x 1000 = 1.000.000
Bei der Multiplikation mit 100.000 zeichnete man ein nach unten offenes Viereck um das entsprechende röm. Zahlzeichen:
X (mit Vierreck/unten offen)
= 10 x 100.000
Additives Bildungsgesetz:
Man spricht bei den röm. Zahlen auch von einem sogenannten additiven Bildungsgesetz. D. h., die röm. Zahlenzeichen müssen zur Interpretation vom Benutzer (Leser) erst noch zusammengerechnet werden. Leider ist dieses additive System nichteinmal konsequent durchgehalten worden, so dass einige Schwierigkeiten (gerade für uns!) auftreten. Arithmetische Rechenoperationen (+ - * :) sind damit außerordentlich unübersichtlich.
*Da lobe ich mir doch unser klareres dezimales System ...
Eine Bildungsvorschrift besagt z. B.: steht ein kleiner Wert direkt (links) vor einem größeren, dann wird er abgezogen (IX = 9 / IC = 99). Steht ein kleiner Wert direkt rechts neben einem größeren (oder mehrere gleichgroße nebeneinander), so wird addiert (CI = 101 / CC = 200).
Die größte "normal" darstellbare röm. Zahl ist 3999 (MMMIM). Dargestellt nach den sogenannten allg. Regeln.
|
röm. Zahlen (nach den allg. Regeln) | |
| I | = 1 |
| II | = 2 |
| III | = 3 |
| IV | = 4 |
| V | = 5 |
| VI | = 6 |
| VII | = 7 |
| VIII | = 8 |
| IX | = 9 |
| X | = 10 |
| XI | = 11 |
| XII | = 12 |
| XIII | = 13 |
| XIV | = 14 |
| XV | = 15 |
| XXI | = 21 |
| XXIX | = 29 |
| XXXIX | = 39 |
| XL | = 40 |
| IL | = 49 |
| L | = 50 |
| C | = 100 |
| CIL | = 149 |
| CC | = 200 |
| D | = 500 |
| M | = 1000 |
| MMMIM | = 3999 |
Der 'kleine Gauß'
Reihen-Summe nach Gauß
Stellen Sie sich vor, Sie sollen die Werte von 1 bis n (Schrittweite 1) addieren.
Also 1+2+3+4 ... n.
Natürlich können Sie diese Werte untereinanderschreiben und brav addieren. Dies kann aber (schon) bei 1 ... 100 sehr lange dauern.
Elegant (und extrem schnell) ist aber die Formel-Lösung (angeblich nach C. F. Gauß).
Carl Friedrich Gauß (dt. Mathematiker *1777 †1855) soll als Schüler schon auf die clevere Idee gekommen sein, für solch eine Aufgabe gleiche Zahlenpaare zu bilden und die Anzahl der Zahlenpaare mit deren Summenwert malzunehmen und dadurch den Rechenaufwand extrem zu minimieren.
Seine Formel dazu lautet: (n+1) * n/2
In (A3) ist die Anzahl der Elemente (n) eingetragen (hier: 100).
In (A8) steht die dazugehörige Berechnungs-Formel [entspricht: (n+1) * n/2 ].
So ergibt die Summe bei n=100 genau 5050.
Bei n=10 sind es 55.
Probieren Sie einmal eigene Werte aus!
Soll von einem anderen Wert als 1 gestartet werden, so kann man sich mit der Berechnung von zwei Zahlenpaar-Summen helfen. Die kleinere Zahlenpaar-Summe wird dann von der größeren abgezogen.
Beispiel: Die Summe der Zahlen von 3..12 wird gesucht.
1. Summe (1..12) = 78.
2. Summe (1..2) = 3.
Erste Summe (78) minus zweite Summe (3) = 75.
Zahlenpaarwert * halbe Anzahl der Elemente = Summe der Einzelwerte.
Diese Formel wird auch als 'der kleine Gauß' bezeichnet.
Die Zahl Pi (3,14~) ist als Wert zur Berechnung von Kreisumfängen und
Umlaufbahnen (Astronomie) etc. bekannt.
Die Reihe der zu Pi gehörigen Dezimalstellen lässt sich dabei bis in's Unendliche fortführen und folgt dabei keinem Muster.
Pi = 4 * (1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 ...)
Je mehr Brüche (wie hier beschrieben!) einbezogen werden, desto genauer wird Pi berechnet.
Pythagoreische Zahlentripel
a² + b² = c². Dass dies in allen rechtwinkligen Dreiecken gilt, ist Schulweisheit.
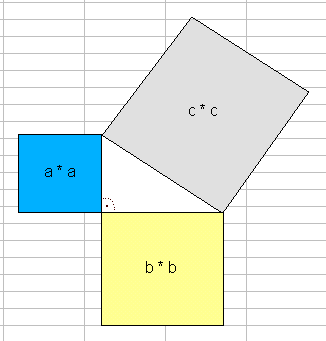
Ein Beispiel dafür ist: 3² + 4² = 5².
Oder:
5² + 12² = 13²
Aber welche Zahlentripel gibt es noch?
Primzahlen - ewiges Mysterium!
Primzahlen sind Zahlen, die nur durch sich selbst oder durch 1 ganzzahlig teilbar sind.
Es gibt nur 2 "Sorten" Primzahlen.
Die einen können gebildet werden als (4 * n) + 1,
die anderen als (4 * n) - 1.
(* Wobei n eine ganze Zahl ist, die aber nicht 'prim' sein muss!).
Beispiele | | |
| (4 * n) +1 | 13 = (4 * 3) +1 | (13-1) / 4 |
| (4 * n) -1 | 31 = (4 * 8) -1 | (31+1) / 4 |
Weiter gilt:
Primzahlen treten nur unregelmäßig auf.
Während im Bereich von 1..100 gleich 25 Primzahlen zu finden sind, gibt es in Bereichen erheblich größerer Zahlen (etwa zw. 10.000 - 10.100) nur noch sehr wenige.
Leonhard Euler (Schweizer Mathematiker *1707 †1783) bewies, dass die Primzahlen, die mit (4 * n) + 1 gebildet werden können, immer auch die Summe zweier Quadrate sind.
Beispiele:
13 = 2² + 3²
Die zweite Gruppe der Primzahlen (4 * n) - 1 lässt sich nicht als Summe zweier Quadrate darstellen.
Interessant ist auch der Versuch, über weitere Formeln (als die obigen) verlässlich Primzahlen zu erzeugen.
Mit: n2+n+41 liefert n stets eine Primzahl. Aber nur, wenn man für n ganzzahlige Werte zwischen 0 - 39 einsetzt (solch eine Liste kann man mit einer kleinen Excel-Tabelle schnell erstellen - siehe unser Beispiel!).
Erkenntnis: n = 40 ergibt schon keine Primzahl mehr.
Übrigens gilt dies auch für die Formel n2+n+17, wobei n kleiner sein muss als 16.
| n | n2+n+41 |
| 0 | 41 |
| 1 | 43 |
| 2 | 47 |
| 3 | 53 |
| 4 | 61 |
| 5 | 71 |
| 6 | 83 |
| 7 | 97 |
| 8 | 113 |
| 9 | 131 |
| 10 | 151 |
| 11 | 173 |
| 12 | 197 |
| 13 | 223 |
| 14 | 251 |
| 15 | 281 |
| 16 | 313 |
| 17 | 347 |
| 18 | 383 |
| 19 | 421 |
| 20 | 461 |
| 21 | 503 |
| 22 | 547 |
| 23 | 593 |
| 24 | 641 |
| 25 | 691 |
| 26 | 743 |
| 27 | 797 |
| 28 | 853 |
| 29 | 911 |
| 30 | 971 |
| 31 | 1033 |
| 32 | 1097 |
| 33 | 1163 |
| 34 | 1231 |
| 35 | 1301 |
| 36 | 1373 |
| 37 | 1447 |
| 38 | 1523 |
| 39 | 1601 |
31; 331; 3.331; 33.331; 333.331; 3.333.331; 33.333.331; 333.333.331;
Danach bricht aber diese Reihe ab. D. h. die nächste '3-er-Zahl' ist schon nicht mehr prim!
'Das 2-Beiner und 4-Beiner Problem'
Auf einem Bauernhof leben 2-beinige und 4-beinige Tiere. Sagen wir: Hühner und Schweine.
Nun werden uns nur die Anzahl der Beine (insgesamt) und die Zahl der Tiere
(insgesamt) genannt und wir sollen über eine Formel herausbekommen, wie viel
Hühner und Schweine es dort gibt.
Die Formel, um die 2-beinigen Tiere zu ermitteln, lautet:
2 * Anzahl der Tiere - ( Beine / 2 )
Beispiel:
14 Tiere und 32 Beine.
12 Hühner + 2 Schweine (12 * 2 Beine) + (2 * 4 Beine).
Testen Sie die Formel ruhig mit anderen Werten.
T = Anzahl aller Tiere; B = Anzahl aller Beine;
V = Anzahl der Vierbeiner; Z = Anzahl der Zweibeiner.
Für 2-Beiner:
Z=2T-B/2
T=Z+V
B=2Z+4V
2Z=4T-B
Für 4-Beiner:
V=B/2-T
H = Hühner
S = Schweine
H + S = 17 (Hühner und Schweine zusammen ergeben 17 Tiere)
2H + 4S = 50 (Die Summe der Beine der 2-beinigen und die der 4-beinigen ergibt 50)
Letztere Formel will gekürzt werden (Alle Elemente durch 2):
H + 2S = 25
Jetzt kann man gut erkennen, dass die erste Formel (H+S=17) prima eingesetzt werden kann. Heißt, auf der linken Seite nehme ich H+S weg. Auf der rechten Seiten die 17, die ja dem Wert von H+S entspricht, so habe ich auf beiden Seiten eine gleichwertige Operation gemacht ...
S = 25-17
Übrig ist der Wert für die Anzahl der Schweine (S) = 8.
Da die Anzahl der Tiere ja 17 war, muss die Anzahl der Hühner (H) = 9 sein.
Probe zum Schluss: 8x4 + 9x2 = 50.
*Die Lösung ist eindeutig, es gibt also keine alternativen Lösungen.
Ein 'magisches Quadrat' ist eine Rechteck-Konstruktion, in der Zahlen so angeordnet sind, dass sie zumindest in den Reihen- und auch den Spalten- und den beiden Diagonalen-Summen immer den gleichen Wert ergeben.
Beispiel:Albrecht Dürers 'mag. Quadrat' aus seinem Bild "Melancholie" ist besonders pfiffig.
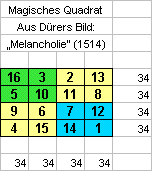
Dürer hat übrigens in der untersten Zeile das Entstehungsjahr des Bildes (1514) untergebracht und ein ganz besonderes 'magisches Quadrat' konstruiert.
So sind nicht nur die Zeilen- und Spaltensummen gleich. Es existieren im Dürer-Quadrat reichlich weitere Möglichkeiten die Summe 34 zu bilden!
*Wir von wispor.de haben 18 Möglichkeiten hier die 34 zu bilden gefunden. Haben Sie mehr entdeckt? Einige besondere Lösungen haben wir unter dem Bild ('mag. Quadrat') versteckt.
Die Buchstaben bedeuten dabei die Felder (oben links mit 'A' [16] im 'mag. Quadrat' beginnend!).
Erstellen Sie doch einmal ein magisches Quadrat.
Z. B. eines '3. Ordnung' mit den Zahlen von 1..9.
Die Zeilen- und Spaltensummen und die Summen der beiden Diagonalen müssen dabei jeweils 15 ergeben!
*Magische Quadrate ungerader Ordnung (3er, 5er ...) sind leichter zu erstellen, als die gerader Ordnung (4er, 6er ...).
**Wenn Sie ermitteln wollen, wie die Zeilen-, Spaltensumme für ein zu erstellendes 'magisches Quadrat' sein muss: Nutzen Sie doch ('den kleinen Gauß') weiter unten.
Beispiel: Sie wollen ein mag. Quadrat 5ter Ordnung erstellen.
Sie benötigen also 5 Reihen a 5 Zahlen, ergo die Zahlen von 1 bis 25.
n = 25 | (n+1) * n/2 | 26 * 12,5 = 325
325 dividiert durch die Anzahl der Zeilen (5) = 65.
Zeilen- und Spaltensumme müssen also für dieses mag. Quadrat 5ter Ordnung jeweils 65 sein.
Die 73 ist die beste Zahl!
In der 73. Folge (The Alien Parasite Hypothesis) der amerik. Kultserie für 'Nerds': 'The Big Bang Theory' erklärt Dr. Dr. Sheldon Lee Cooper, dass die 73 die 'beste' Zahl ist:
73 ist die 21. Primzahl.
Die Spiegelzahl der 73, die 37, ist wiederum eine Primzahl (die 12.).
[Die 73 ist also auch noch eine 'Mirpzahl' (eine Zahl, die rückwärts gelesen wiederum eine Primzahl ergibt; hier: 37).
*Mirp meint Prim (umgekehrt!).
Die Spiegelzahl der 12 ist die 21 und 21 erhält man auch, wenn man 7 mit 3 multipliziert
Überträgt man die 73 in's Binärformat, liest sie sich als 1001001 - dies ergibt ein Palindrom.
Die 73 ist auch die 18. glückliche Zahl.
*Eine 'glückliche Zahl' (1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, ...) ist eine Zahl - die man auch 'überlebende Zahl' nennen könnte ;) -, die bei folgendem Verfahren nicht gelöscht wird:
Erstens streicht man aus der Menge der 'natürlichen Zahlen' alle geraden Zahlen.
(Beispiel hier: 1-25)
*Die 'überlebende' Zahl ist jetzt die 3.
Zweitens streicht man nun jede 3. der neuen Reihe (1,3,5,7,9,11,13,15,17,19,21,23,25).
Also die: 5,11,17,23. Übrig bleiben: 1,3,7,9,13,19,21,25.
*Die 'überlebende' Zahl ist jetzt die 7.
Drittens streicht man nun jede 7. der neuen Reihe (1,3,7,9,13,19,25).
Also die: 21. Übrig bleiben: 1,3,7,9,13,19,25.
*Die 'überlebende' Zahl ist jetzt die 9.
**Die Kenntnis dieser Regel ist sehr wichtig beim 'Josephus-Spiel' und dabei geht es immerhin um's nackte Überleben :) !
Gansgewicht
Aufgabe: Eine Gans wiegt 10 Kg und die Hälfte ihres Gewichtes.
15 Kg ist falsch!
Es würde ja bedeuten, dass die halbe Gans 7,5 Kilo wiegt! Dass 'beisst' sich mit dem Ausgangswert.
Vielleicht nehmen Sie sich einmal 3 Minuten Zeit, ein Stück Papier und einen Stift und versuchen es mit einer kleinen Formel ...
Wenn Sie aber partout nicht auf die Lösung kommen: Unter dem 'St. Isidor'-Bild finden Sie die Lösung.
Lotto 6er
Wie hoch ist die Wahrscheinlichkeit 6 Richtige beim Lotto (6 aus 49) zu erhalten? Anders ausgedrückt, wie viel Lottoreihen müsste man ausfüllen, um mit Sicherheit einen Sechser zu bekommen?
| Lotto | |
| Hier kann natürlich noch gekürzt werden! | |
| 6er | (49*48*47*46*45*44) / 6! |
| 6er | (49*48*47*46*45*44) / 6*5*4*3*2*1 |
| Ein "Vierer" ist natürlich viel leichter zu erhaschen! | |
| 4er | (49*48*47*46) / 4! |
| 4er | (49*48*47*46) / 4*3*2*1 |
'Stargate'™
Hinweis:
Ich gehe von 40 Symbolen auf den 'Sternentoren' aus.
*Hab' sie abgezählt!
| 'Stargate'™ | |
| Hier kann natürlich noch gekürzt werden! | |
| 7-Symbolanwahl | (40*39*38*37*36*35*34) / 7! |
| 7-Symbolanwahl | (40*39*38*37*36*35*34) / 7*6*5*4*3*2*1
= 18.643.560 Sternentoradressen (7:40) |
*Für eine Berechnung klicken Sie auf 'Fakultät von ...'
xx sss xxx
*Für eine Berechnung klicken Sie auf 'Grenze eingeben ...'
xx sss xxx
*Für eine Berechnung klicken Sie auf 'Quadrat von ...'
xx sss xxx
| ___________________________________________________________________________ |
- lexikalischer Auskunftsdienst / Münster (Westfalen)